圆锥的侧面积公式
的有关信息介绍如下:正圆锥的侧面积公式: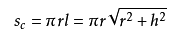
上式中,h为圆锥的高,st为圆锥的表面积,sc为侧面积。正圆锥的侧面可以展开为平面上的一个扇形。这个扇形所在的圆半径就是圆锥的斜高,对应的圆弧长为底部圆形的周长。因此可以用上述公式求正圆锥的侧面积。
其他条件下,圆锥的侧面积可用以下公式:
圆锥的侧面积=母线的平方×π×(360分之扇形的度数)
圆锥的侧面积=1/2×母线长×底面周长
圆锥的侧面积=π×底面圆的半径×母线

扩展资料:
圆锥的表面积=底面积+侧面积 S=πr²+πrl (注l=母线)
圆锥的体积=1/3底面积乘高 或 1/3πr^2*h
圆锥是一种几何图形,有两种定义。解析几何定义:圆锥面和一个截它的平面(满足交线为圆)组成的空间几何图形叫圆锥。
立体几何定义:以直角三角形的直角边所在直线为旋转轴,其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。旋转轴叫做圆锥的轴。
垂直于轴的边旋转而成的曲面叫做圆锥的底面。不垂直于轴的边旋转而粗纯成的曲稿凳坦面叫做圆锥的侧面。无论旋转到什么位置,不垂直于轴的边都叫做圆锥的母线。(边是指直角三角形两个旋转边)
正圆锥可以定义为一个直角三角形绕其中一条直角边旋转一周得到的几何体,这个直角三角形的斜边称为圆锥的母线。顶点键桐在底面的投影不在圆心,这样的圆锥称为斜圆锥。正圆锥可以由平面截圆锥面得到,斜圆锥则不能。倾斜平面截取圆锥面得到的几何形体叫做椭圆锥。
参考资料来源:百度百科-圆锥体



