整数的概念是什么？

整数的概念是什么？

整数是正整数+0+负整数，也就是除了分数、小数，例如：4、5、6、0、-4、-8等都是整数。

整数集由全体整数构成：

-9、-8、-7、…、-n、…（n为非零自然数）为负整数。

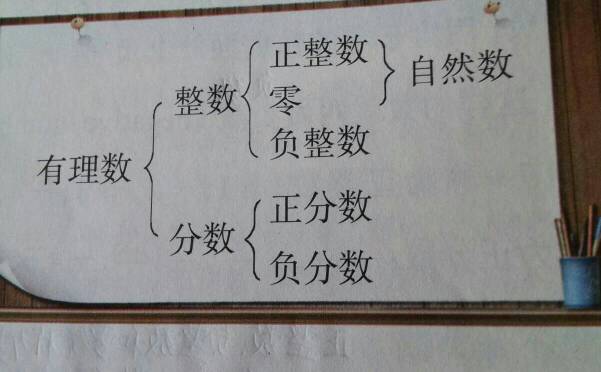
整数系包括来正整数、零与负整数 。

整数有三大类：

1、正整数，就是大于0的整数，例如1，2，3······直到n

2、负整数，就是小于0的整数，例如-1，-2，-3······直到-n。（n为正整数）

3、0不是正整数，也不是负整数，是介于正整数和负整数的数。

扩展资料：

整数中，能够被2整除的数，叫做偶数。不能被2整除的数则叫做奇数。即当n是整数时，偶数可表示为2n(n 为整数)；奇数则可表示为2n+1(或2n-1)。

偶数包括正偶数（亦称双数）、负偶数和0。所有整数不是奇数，就是偶数。

在十进制里，我们可用看个位数的方式判断该数是奇数还是偶数：个位为1,3,5,7,9的数为奇数；个位为0,2,4,6,8的数为偶数。

利用皮亚诺公理可以对正整数及N*进行如下猜笑描述:

任何一个满足下列条件的非空集猜基合叫做正整数集合，记作N*。如果

Ⅰ 1是正整数；穗兆谨

Ⅱ 每一个确定的正整数a，都有一个确定的后继数a' ，a'也是正整数（数a的后继数a‘就是紧接在这个数后面的整数（a+1）。例如，1‘=2，2’=3等等。）；

Ⅲ 如果b、c都是正整数a的后继数，那么b = c；

Ⅳ 1不是任何正整数的后继数；

Ⅴ 设S⊆N*，且满足2个条件（i）1∈S；（ii）如果n∈S，那么n'∈S。那么S是全体正整数的集合，即S=N*。(这条公理也叫归纳公理，保证了数学归纳法的正确性)

皮亚诺公理对N*进行了刻画和约定，由它们可以推出关于正整数的各种性质。

负整数是小于0的整数；

负整数与负整数的和仍为负整数；

负整数与负整数的积为正整数；

负整数存在最大值-1，不存在最小值；

负整数在实数范围内不能开平方，不能开偶数次方，但是可以开奇数次方；

负整数在虚数范围内可以进行开方运算，i*i=-1。

0是介于-1和1之间的整数。是最小的自然数，也是有理数。0既不是正数也不是负数，而是正数和负数的分界点。0没有倒数，0的相反数是0，0的绝对值是0，0的平方根是0,0的立方根是0，0乘任何数都等于0，除0之外任何数的0次方等于1。0不能作为分母出现，0的所有倍数都是0。0不能作为除数。

中国古代的筹算数码中没有“零”，遇到“零”就空位。比如“6708”就可以表示为“┴　╥ ”。数字中没有“零”，是很容易发生错误的。所以后来有人把铜钱摆在空位上，以免弄错，这或许与“零”的出现有关。

但在我国古代文字中，中文的“零”字出现很早。不过那时它不表示“空无所有”，而只表示“零碎”、“不多”的意思。如“零头”、“零星”、“零丁”。

“一百零五”的意思是：在一百之外，还有一个零头五。但中国古代并没有0这个字体，只有中文的字体零来表示。随着阿拉数字的引进。“105”恰恰读作“一百零五”，“零”字与“0”恰好对应，“零”也就具有了“0”的含义。0在我国古代叫做金元数字。

参考资料：百度百科---整数