蝶形定理

蝶形定理

蝴蝶定理（Butterfly theorem），是古典欧氏平面几何的最精彩的结果之一。这个命题最早出现在1815年，而“蝴蝶定理”这个名称最早出现在《美国数学月刊》1944年2月号，题目的图形象一只蝴蝶。这个定理的证法多得不胜枚举，至今仍然被数学热爱者研究，在考试中时有出现各种变形。

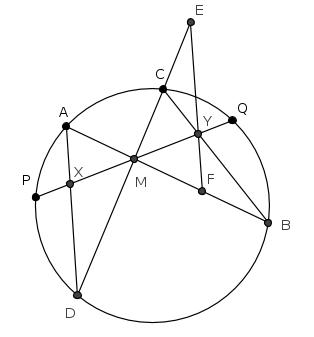
最基本的叙述为：设M为圆内弦PQ的中点，过M作弦AB和CD。设AD和BC各相交PQ于点X和Y，则M是XY的中点。

这个命题最早作为一个征解问题出现在公元1815年英国的一本杂志《男士日记》（Gentleman's Diary）39-40页上。登出的当年,英国一个自学成才的中学数学教师W.G.霍纳（他发现了多项式方程近似根的霍纳法）给出了第一个证明，完全是初等的；另一个个证明由理查德·泰勒（Richard Taylor）给出。另外一种早期的证明由M.布兰德（Miles Bland）在《几何问题》（1827年）一书中给出。最为简洁的证法是射影几何的证法，由英国的J·开世在"A Sequel to the First Six Books of the Elements of Euclid"（中译：近世几何学初编，李俨译，上海商务印书馆 1956 ）给出，只有一句话，用的是线束的交比。1981年，Crux杂志刊登了K.萨蒂亚纳拉亚纳（Kesirajn Satyanarayana）用解析几何的一种比较简单的方法（利用直线束，二次曲线束）。

该定理实际上是射影几何中一个定理的特殊情况，有多种推广：

1. M，作为圆内弦是不必要的，可以移到圆外。

2. 圆可以改为任意圆锥曲线。

3. 将圆变为一个完全四角形，M为对角线交点。

4. 去掉中点的条件，结论变为一个一般关于有向线段的比例式，这对2，3均成立。

以下是证明过程

如图，过Y作EF//AD，交DC的延长线于E，交AB于F。

∵ ∠ADE = ∠ABC，又 ∠ADE = ∠FED （内错角相等）

∴ ∠ABC = ∠FED

∴ C,E,B,F 四点共圆

由相交弦定理可得 EY × YF = BY × YC

显然 ΔAMD ∽ ΔFME , ΔAMX ∽ ΔFMY , ΔXMD ∽ ΔYME

∴ MX² : (AX × XD) = MY² : (EY × YF) = MY² : (BY × YC)

由相交弦定理可得 AX × XD = PX × XQ , BY × YC = PY × YQ

∴ MX² : (MX² + PX × XQ) = MY² : (MY² + PY × YQ)

∵ MX² + PX × XQ = (PM - PX)² + PX × (2PM - PX) = PM²

MY² + PY × YQ = (MQ - YQ)² + PY × (2QM - PY) = QM²

∴ MX² : PM² = MY² : MQ² , MX : PM = MY : MQ

又 PM = MQ

∴ MX = MY , 得证