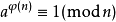欧拉线的详细证明方法

欧拉线的详细证明方法

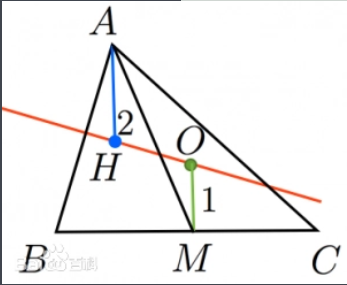
如图所示，设AM为△ABC的中线，H、O分别是垂心和外心，连接AH、OM，则OM⊥BC，AH⊥BC

∴AH∥OM

连接OB、OC，易证∠BAC=∠BOC/2=∠COM

∴OM=OCcos∠COM=Rcos∠BAC（R是△ABC外接圆半径）

又连接BH并延长交AC于D，则BD⊥AC

∴AH=AD/cos∠CAH=ABcos∠BAC/sin∠ACB=2Rcos∠BAC

∴AH=2OM

设OH和AM交于G，则△AHG∽△MOG

∴AG:GM=AH:OM=2:1

∴G是△ABC的重心，即O、H、G三点共线，且GH:GO=AG:GM=2:1

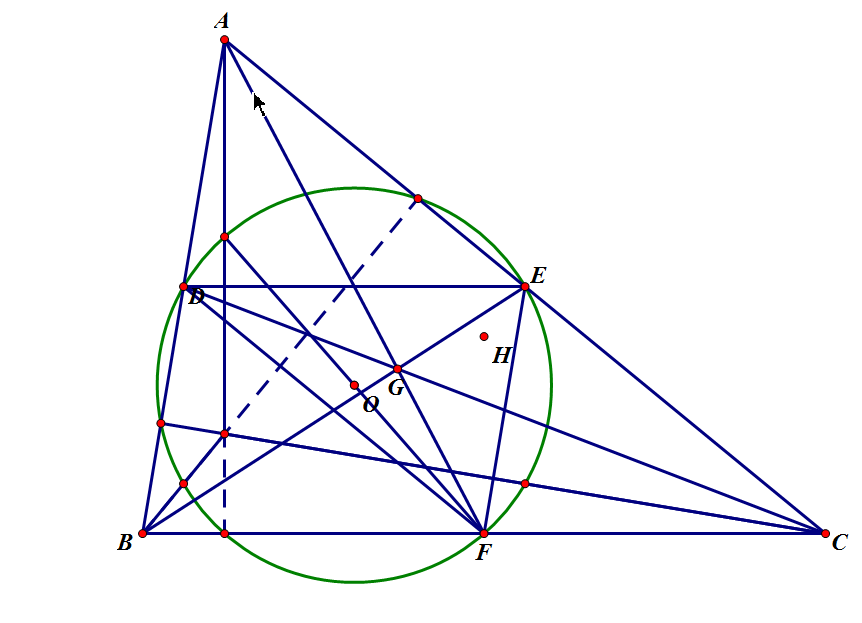
然后证明九点圆心也在线上，如下图，DEF为△ABC中点，OGH为△DEF外心、重心、垂心，则用线束可证G也是△ABC重心，DH,EH,FH分别垂直于△ABC三边且DEF为三角形ABC三边中点，∴H为△ABC外心，DO=EO=FO,∴O为△ABC九点圆心，∴九点圆心也在欧拉线上