求函数定义域的方法…
的有关信息介绍如下:设D、M为两个非空实数集,如果按照某个确定的对应法则f,使得对于集合D中的任意一个数x,在集合M中都有唯一确定的数y与之对应,那么就称f为定义在集合D上的一个函数,记做y=f(x)。
其中,x为自变量,y为因变量,f称为对应关系,集合D成为函数f(x)的定义域,为函数f的值域,对应关系、定义域、值域为函数的三要素。
本质为任意角的集合与一个比值的集合的变量之间的映射,通常的三角函数是在平面直角坐标系中定义的,其定义域为整个实数域,另一种定义是在直角三角形中,但并不完全,现代数学把它们描述成无穷数列的极限和微分方程的解,将其定义扩展到复数系。
其主要根据为:
1、分式的分母不能为零。
2、偶次方根的被开方数不小于零。
3、对数函数的真数必须大于零。
4、指数函数和对数函数的底数必须大于零且不等于1。
函数的定义域定义方法:
自然定义域,若函数的对应关系有解析表达式来表示,则使解析式有意义的自变量的取值范围称为自然定义域。例如函数:
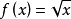
要使函数解析式有意义,则:
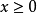
因此函数的自然定义域为:
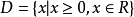
参考资料来源:百度百科-函数定义域



