共轭复数性质

共轭复数性质

1、复数的加、减、乘、除运算法则 

设z1＝a＋bi，z2＝c＋di(a，b，c，d∈R)，则 

①加法：z1＋z2＝(a＋bi)＋(c＋di)＝(a＋c)＋(b＋d) ； 

②减法：z1－z2＝(a＋bi)－(c＋di)＝(a－c)＋(b－d) ； 慧凳

③乘法：z1•z2＝(a＋b )•(c＋d )＝(ac－bd)＋(ad＋bc) ； 

④除法：

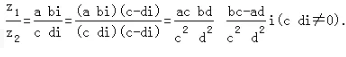
2、共轭法则

z=x+iy的共轭，标注为z*就是共轭数z*=x-iy

即：zz*=（x+iy)(x-iy)=x2-xyi+xyi-y2i2=x2+y2

即，当一个复数乘以他的共轭数，结果是实数。

z=x+iy 和 z*=x-iy 被称作共轭对。

现在用复数前迟旅乘法计算(a+bi)(a-bi)得到(a+bi)(a-bi)=a2+b2, 结果是非负实数. 这个结果很重要, 因为两个复数相乘后变成了实数. 这两个复数a-bi与a+bi实部相等, 虚部互为相反数, 称它们互为共轭复数

扩展资料

复数的加法、减法、乘法运算可以类比多项式运算，只要注意i2=-1即可. 

计算(4-3i)(-5+4i) 

【解析】(4-3i)(-5+4i)=-20+16i+15i-12i2=-20+31i+12=18+31i 

如果两个复数相等a+bi=c+di, 移项后得到a+bi-(c+di)=0, 根据复数的减法有(a-c)+(b-d)i=0. 复数等于零旦咐, 只有实部和虚部都为零, 于是得到a=c, b=d. 因此两个复数相等意味着实部与实部相等, 虚部与虚部相等。

参考资料来源：百度百科-共轭复数