为什么狄利克雷函数是周期函数？

为什么狄利克雷函数是周期函数？

如下：

狄利克雷函数是周期函数证明：取T为任意一个确定的有理数，则当x是有理数时f(x)=1，且缺简x+T是有理数，故f(x+T)=1，即f(x)=f(x+T)；当x是无理数时，f(x)=0，且x+T是无理数，故有f(x+T)=0，即f(x)=f(x+T)。综上，狄利克雷函数是周期函数。

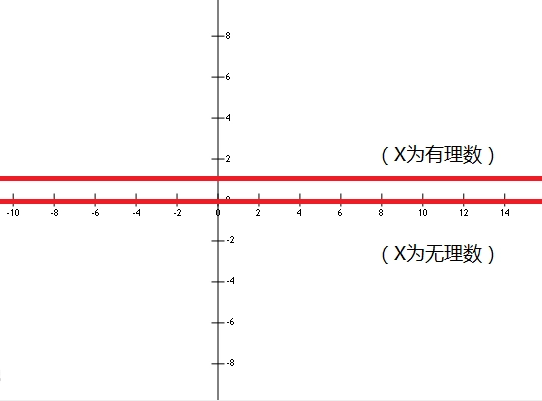
狄利克雷函数基本性质：

1、定义域为整个实数域R。

2、值桥空域伏消裤为{0,1}。

3、函数为偶函数。

4、无法画出函数图像，但是它的函数图像客观存在。

5、以任意正有理数为其周期，无最小正周期（由实数的连续统理论可知其无最小正周期）。