有效久期、麦考林久期和修正久期有什么区别？

有效久期、麦考林久期和修正久期有什么区别？

1、对时间价值的考虑不同：

修正久期在麦考利久期的基础上，考虑了久期的时间价值，可以说对麦考利久期的动态修正。

2、数学模型不同：

有效久期是债券价格曲线的切线，衡量的是区间价格变动的敏感程度，计算方法类似弹性可用于求已知价格变动的债券。

有效久期是指债券或其他金融工具的价格对利率敏感度的直接计算方法。即通过计算由利率的微小变动带来的债券价格差异而得出的价格变动百分比。

久期是表示对未来收入的加权等待时间,也是债券价格对利率的敏感程度。  

有效久期是债券价格曲线的切线，衡量的是区间价格变动的敏感程度。

3、计算公式不同：

麦考林久期、修正久期分零息与付息债券,对于零息MAC DUR=到期时间(T),修正久期=T/[1+(Y/N)]，Y表示年利率,N表计算复利次数.对于付息债券，MAC DUR=加权公式。就是每期支付折现除以现值乘与期数那公式。

修正久期=MAC/[1+(Y/N)]，无期限债券,永续,特殊方法计算。

麦考利久期计算方法

麦考利久期等于债券每次息票或债券本金支付时间的加权平均 。

假设一张T年期债券，t时刻的现金支付为

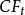
（1≤t≤T），到期收益率为y，债券价格为P。

权重

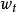
与时间t 所发生的现金流（

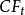
）有关，表示为：

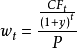
公式右边的分子代表在时间 t 所发生的现金流量的现值。分母代表债券所有支付的值。这些权重和为1.0，因为以到期收益率贴现的现金流总额等于债券价格 [3]  。

用这些值来计算所有债券支付时间的加权平均，就可以得到麦考利久期公式，表示为：

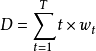
麦考利久期定理：关于麦考利久期与债券的期限之间的关系存在以下6个定理：

定理1：只有贴现债券的麦考利久期等于它们的到期时间。

定理2：直接债券的麦考利久期小于或等于它们的到期时间。只有仅剩最后一期就要期满的直接债券的麦考利久期等于它们的到期时间，并等于1。

定理3：统一公债的麦考利久期等于（1+1/r），其中r是计算现值采用的贴现率。

定理4：在到期时间相同的条件下，息票率越高，久期越短。

定理5：在息票率不变的条件下，到期时期越长，久期一般也越长。

定理6：在其他条件不变的情况下，债券的到期收益率越低，久期越长。

扩展资料：

久期用途

在债券分析中，久期已经超越了时间的概念。修正久期大的债券，利率上升所引起价格下降幅度就越大，而利率下降所引起的债券价格上升幅度也越大。可见，同等要素条件下，修正久期小的债券比修正久期大的债券抗利率上升风险能力强；但相应地，在利率下降同等程度的条件下，获取收益的能力较弱。

正是久期的上述特征给我们的债券投资提供了参照。当我们判断当前的利率水平存在上升可能，就可以集中投资于短期品种、缩短债券久期；而当我们判断当前的利率水平有可能下降，则拉长债券久期、加大长期债券的投资，这就可以帮助我们在债市的上涨中获得更高的溢价。

参考资料：

百度百科   有效久期

百度百科   麦考利久期

百度百科   修正久期