在平面直角坐标系中,O为原点,点A(-2,0),点B(0,2)点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,

在平面直角坐标系中,O为原点,点A(-2,0),点B(0,2)点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,

这个题是在图形旋转过程中,考查了全等三角形的判定与性质,勾股定理,三角形的外角性质,30度角所对的直角边等于斜边的一半等知识,而找到使点P的纵坐标最大时点P的位置是解决最后一个问题的关键.第一问(1)利用勾股定理即可求出AE',BF'的长.

(2)运用全等三角形的判定与性质,三角形的外角性质就可解决问题.

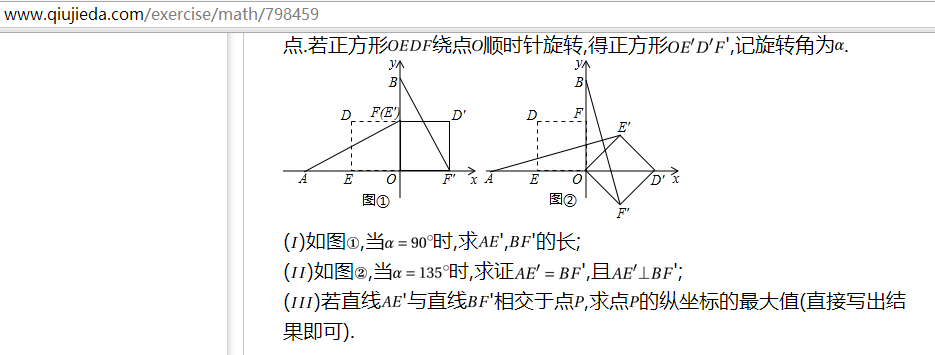
解：（1）当α=90度是，点E‘与点F重合，因为点A（-2,0），点B（0,2），所以OA=OB=2，详细的答案看这里哦http://www.qiujieda.com/exercise/math/798459在平面直角坐标系中,O为原点,点A(-2,0),点B(0,2)点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE'D'F,记旋转角为α.(1)如图1,当α=90度时,求AE',BF'的长;

(2)如图2,当α=135度时,求证AE'=BF‘,且AE'垂直BF’;

(3)若直线AE'与直线BF'相交于点P,求点P的纵坐标的最大值(直接写出结果即可).