对数函数的换底公式是什么
的有关信息介绍如下:换底公式是一个比较重要的公式,在很多对数的计算中都要使用,也是高中数学的重点。另有两个推论。loga(b)表示以a为底的b的对数。
如果ax =N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作x=logaN,读作以a为底N的对数,其中a叫做对数的底数,N叫做真数。
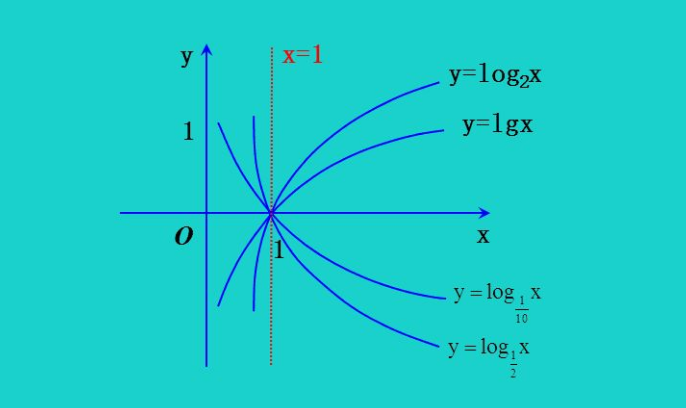
一般地,函数y=logaX(a>0,且a≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数。
其中x是自变量,函数的定义域是(0,+∞),即x>0。它实际上就是指数函数的反函数,可表示为x=ay。因此指数函数里对于a的规定,同样适用于对数函数。

扩展资料:
但是,如果是不等于1的正实数,这个定义可以扩展到在一个域中的任何实数(参见幂)。类似的,对数函数可以定义于任何正实数。对于不等于1的每个正底数,有一个对数函数和一个指数函数,它们互为反函数。
对数可以简化乘法运算为加法,除法为减法,幂运算为乘法,根运算为除法。所以,在发明电子计算机之前,对数对进行冗长的数值运算是很有用的,它们广泛的用于天文、工程、航海和测绘等领域中。它们有重要的数学性质而在今天仍在广泛使用中。
参考资料来源:百度百科-对数函数