幂函数的导数是什么？

幂函数的导数是什么？

幂函数导数公式的证明：

y=x^a。

两边取对数lny=alnx。

两边对x求导(1/y)*y'=a/x。

所以y'=ay/x=ax^a/x=ax^(a-1)。

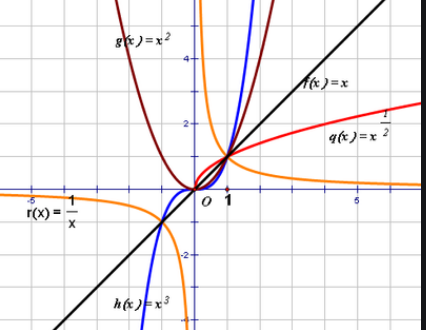
特性介绍：

对于a的取值为非零有理数，有必要分成几种情况来讨论各自的特性：

首先我们知道如果a=p/q，且p/q为既约分数（即p、q互质），q和p都是整数，则x^(p/q)=q次根号下（x的p次方），如果q是奇数，函数的定义域是R，如果q是偶数，函数的定义域是[0,+∞）。

当指数a是负整数时，设a=-k，则y=1/(x^k)，显然x≠0，函数的定义域是（－∞，0)∪(0,+∞)。因此可以看到x所受到的限制来源于两点，一是有可能作为分母而不能是0，一是有可能在偶数次的根号下而不能为负数，那么我们就可以知道：

a小于0时，x不等于0。

a的分母为偶数时，x不小于0。

a的分母为奇数时，x取R。