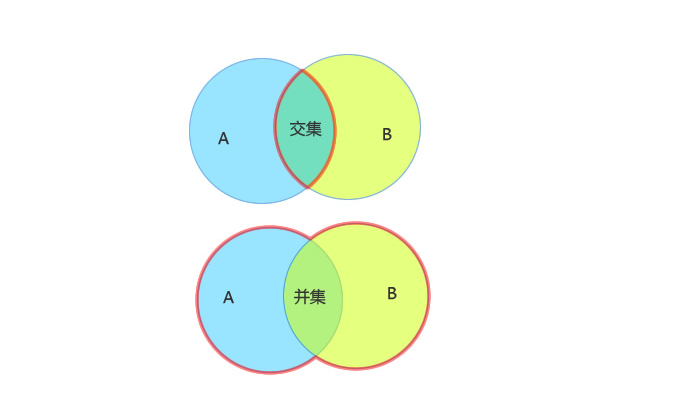
Simone什么是数学里面的隔板法
的有关信息介绍如下：
隔板法就是在n个元素间的（n-1）个空中插入若干个（b）个板，可以把n个元素分成（b+1）组的方法。应用隔板法必须满足三个条件：（1）这n个元素必须互不相异（2）所分成的每一组至少分得一个元素（3）分成的组别彼此相异组合不排列的情况可以用隔板法例如：某校组建一球队需16人，该校共10个班级，共有几种情况？解：（16-1）p（10-1）=1816214400种例1.求方程x+y+z=10的正整数解的个数。〔分析〕将10个球排成一排，球与球之间形成9个空隙，将两个隔板插入这些空隙中（每空至多插一块隔板），规定由隔板分成的左、中、右三部分的球数分别为x、y、z之值（如下图）。则隔法与解的个数之间建立了一一对立关系，故解的个数为c92=36（个）。
